General Policy Composition

Improving Diffusion-based or Flow-based Robot Policies
via Test-time Distribution-level Composition

Compose Your Policies!
Improving Diffusion-based or Flow-based Robot Policies via Test-time Distribution-level Composition

Jiahang Cao^*1,2,3, Yize Huang^*1,4, Hanzhong Guo¹, Rui Zhang¹, Mu Nan¹,

Weijian Mai¹, Jiaxu Wang⁵, Hao Cheng⁵, Jingkai Sun¹, Gang Han²,

Wen Zhao², Qiang Zhang², Yijie Guo², Qihao Zheng³, Chunfeng Song³,

Xiao Li⁴, Ping Luo¹, Andrew F. Luo ^{1\( \ddagger \)}

¹The University of Hong Kong ²Beijing Innovation Center of Humanoid Robotics ³Shanghai AI Lab

⁴Shanghai Jiaotong University ⁵The Hong Kong University of Science and Technology

^*Equal contribution ^\(\ddagger\)Corresponding Author

Paper arXiv Code

Abstract

Diffusion-based models for robotic control, including vision-language-action (VLA) and vision-action (VA) policies, have demonstrated significant capabilities. Yet their advancement is constrained by the high cost of acquiring large-scale interaction datasets. This work introduces an alternative paradigm for enhancing policy performance without additional model training. Perhaps surprisingly, we demonstrate that the composed policies can exceed the performance of either parent policy. Our contribution is threefold: (I) First, we establish a theoretical foundation showing that the convex composition of distributional scores from multiple diffusion models can yield a superior one-step functional objective compared to any individual score. A Grönwall-type bound is then used to show that this single-step improvement propagates through entire generation trajectories, leading to systemic performance gains. (II) Second, motivated by these results, we propose General Policy Composition (GPC), a training-free method that enhances performance by combining the distributional scores of multiple pre-trained policies via a convex combination and test-time search. GPC is versatile, allowing for the plug-and-play composition of heterogeneous policies, including VA and VLA models, as well as those based on diffusion or flow-matching, irrespective of their input visual modalities. (III) Third, we provide extensive empirical validation. Experiments on Robomimic, PushT, and RoboTwin benchmarks, alongside real-world robotic evaluations, confirm that GPC consistently improves performance and adaptability across a diverse set of tasks. Further analysis of alternative composition operators and weighting strategies offers insights into the mechanisms underlying the success of GPC. These results establish GPC as a simple yet effective method for improving control performance by leveraging existing policies.

Motivation

Motivation Illustration: VLA and VA policies are powerful but rely on costly large-scale training. Theoretically, we show that combining distributional scores of pre-trained policies can yield a single-step error drop that propagates stably along the overall trajectory, enabling General Policy Composition (GPC) --- a training-free method to boost policy performance via convex combination. GPC is versatile, allowing for the plug-and-play composition of heterogeneous policies, including VA and VLA models, as well as those based on diffusion or flow-matching, irrespective of their input visual modalities.

Mathematical Foundation

Overview

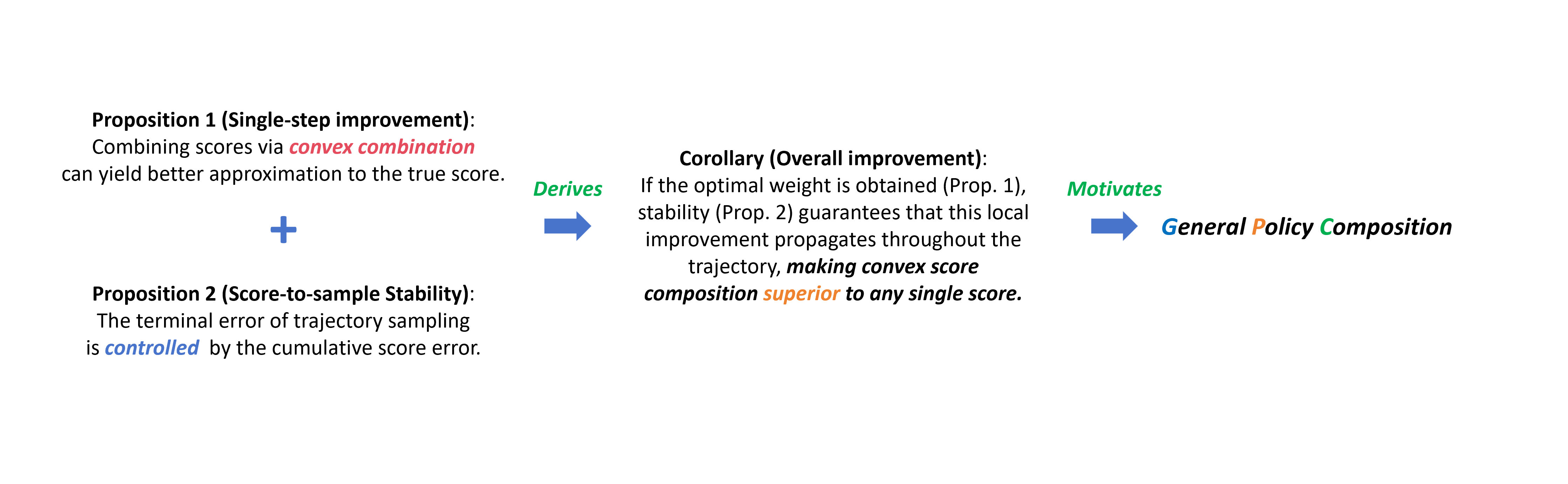
cOverview of Mathematics Foundation: We provide a high-level description of the math foundation of General Policy Composition framework, outlining how function-level (single step improvement) and system-level (overall trajectory improvement) analyses together motivate our approach.

Proposition 1: Function-level Single-step Improvement

Proposition 1 establishes that a proper convex combination of distributional scores can yield a smaller single-step error than either individual score estimator.

Proposition 2: System-level Stability

System-level Proposition 2 and Corollary

Proposition 2 leverages a Grönwall-type inequality to show that the terminal error grows at most exponentially with the Lipschitz constants, and is directly bounded by the integrated score error.

Corollary: Tighter Terminal-state Bound

Corollary 1. Once functional-level improvement is established by obtaining an optimal weight (Prop. 4.1), stability ensures this advantage propagates along the trajectory (Prop. 4.2), making convex score composition provably superior to relying on individual scores.

Method

Overview

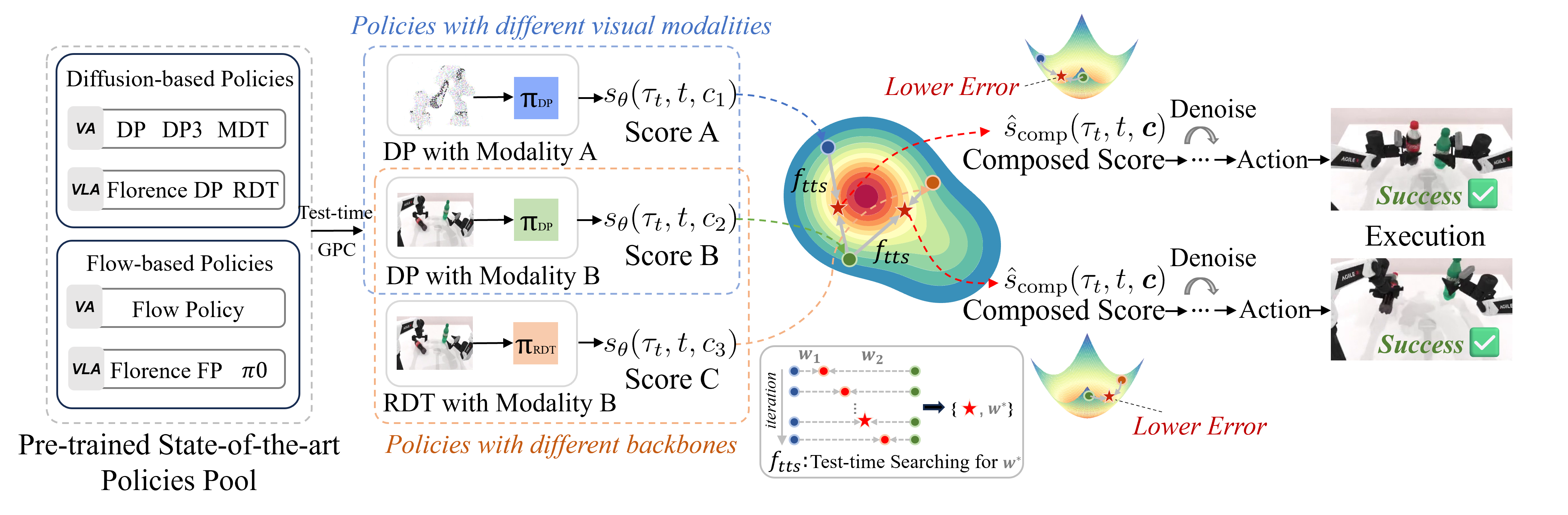
Overview of our proposed General Policy Composition. Combining distributional scores from pre-trained diffusion-based or flow-based policies on different conditions (e.g., visual modalities and network backbones), GPC can generate expressive and adaptable action trajectories through convex score combination without additional training.

Experiments

Main Results

Task: Robomimic and PushT

Experiemnt Settings: There are two variations and we run 200 trials for each variation: (1) Base Diffusion-based and Flow-based Policies (e.g., DP, Flow Policy, Pi-0). The policies are pre-trained based on their original codebase. (2) Composed Policies via GPC. Composed policies are combined via GPC during test-time.

Score Metric: We calculate the average success rate.

TABLE I: Experiment results on Robomimic and PushT.
The table shows the success rate ↑. Our GPC yields a noticeable average improvement compared with the base policies.

Method	Generative Mode	Model Type	Robomimic			PushT	Average
			Can	Lift	Square	PushT	Avg.
Base Policies
Diffusion Policy (DP)	Diffusion	VA	34.50	98.50	2.00	21.75	39.19
Mamba Policy (MP)	Diffusion	VA	5.00	98.50	3.00	12.06	29.64
Flow Policy (FP)	Flow Matching	VA	95.00	13.00	77.50	54.25	59.94
Florence Policy-D	Diffusion	VLA	61.50	97.00	46.50	40.00	61.25
Florence Policy-F	Flow Matching	VLA	89.00	98.50	88.50	39.38	78.84
π0	Flow Matching	VLA	96.50	99.00	92.50	57.69	86.42
Composed Policies via Convex Score Combination
DP + MP	Diffusion	VA & VA	34.50	99.50	8.00	23.63	41.41 (+2.22%)
Florence-Policy-D + DP	Diffusion	VLA & VA	62.50	100.00	61.50	43.06	66.76 (+5.51%)
Florence-Policy-D + MP	Diffusion	VLA & VA	63.00	100.00	54.50	40.88	64.60 (+3.35%)
Florence-Policy-F + FP	Flow Matching	VLA & VA	98.50	98.50	92.50	56.06	86.39 (+7.55%)
π0 + FP	Flow Matching	VLA & VA	99.50	100.00	94.00	62.25	88.94 (+2.52%)

Task: RoboTwin 2.0

Experiemnt Settings: There are two variations and we run 100 trials for each variation: (1) Base Diffusion-based Policies (e.g., DP, DP3, RDT). (2) Composed Policies via GPC.

Score Metric: We calculate the average success rate.

Table II: Experiment results on RoboTwin with 6 diverse bimanual manipulation tasks.
GPC achieves an obvious increase with up to 7% improvement on the success rate.

Method	Model Type	Hanging Mug	Open Laptop	Place Burger Fries	Put Object Cabinet	Stack Bowls Three	Turn Switch	Average
Base Policies
DP_img	VA	0.10	0.74	0.49	0.56	0.52	0.38	0.46
DP_pcd	VA	0.21	0.93	0.72	0.71	0.64	0.71	0.65
RDT	VLA	0.13	0.69	0.46	0.32	0.47	0.30	0.40
Composed Policies via Convex Score Combination
DP_img + DP_pcd	VA & VA	0.23	0.93	0.78	0.82	0.71	0.71	0.70 (+5%)
RDT + DP_img	VLA & VA	0.18	0.80	0.57	0.59	0.66	0.38	0.53 (+7%)
RDT + DP_pcd	VLA & VA	0.36	0.94	0.83	0.78	0.73	0.71	0.72 (+7%)

Visualization of Real World Experiments.

Experiemnt Settings: There are two variations and we run 20 trials for each policy for evaluation: (1) Base Diffusion-based Policies (e.g., DP, DP3). (2) Composed Policies via GPC.

Task: Clean Table

DP fails ❌

DP3 fails ❌

GPC succeeds ✅

Task: Place Bottles

DP fails ❌

DP3 succeeds ✅

GPC succeeds ✅

Task: Hang Mug

DP succeeds ✅

DP3 fails ❌

GPC succeeds ✅

Task: Punch Holes

DP fails ❌

DP3 fails ❌

GPC succeeds ✅

Influence of Weight Configurations on GPC Performance

To analyse how do different weight configurations influence the performance of GPC across various scenarios, we evaluate GPC performance across multiple tasks under different weight configurations as follows.

Table III: Experiment results of our method under different composition configurations.
These results highlight GPC's versatility and the importance of weight tuning across policies.

Scenario	Task	DP_img	DP_pcd	Weight Scheduling in GPC (weight of DP_img)									Δ
Scenario	Task	DP_img	DP_pcd	0.1*	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	Δ
Both Policies Perform Well	Empty Cup Place	0.42	0.62	0.70	0.86	0.84	0.86	0.84	0.84	0.76	0.68	0.61	+24%
	Dual Bottles Pick (Hard)	0.49	0.64	0.69	0.63	0.71	0.66	0.64	0.65	0.63	0.56	0.58	+7%
	Shoe Place	0.37	0.36	0.47	0.52	0.56	0.59	0.60	0.59	0.59	0.53	0.41	+23%
Both Policies Perform Bad	Dual Shoes Place	0.08	0.23	0.19	0.17	0.19	0.20	0.20	0.17	0.16	0.14	0.09	+0%
Both Policies Perform Bad	Pick Apple Messy	0.05	0.26	0.25	0.17	0.21	0.15	0.13	0.08	0.08	0.06	0.08	+0%
Policy A > Policy B	Dual Bottles Pick (Easy)	0.77	0.36	0.52	0.64	0.70	0.75	0.82	0.81	0.80	0.85	0.80	+8%
Policy A < Policy B	Block Hammer Beat	0.00	0.76	0.61	0.30	0.18	0.15	0.12	0.07	0.00	0.00	0.00	+0%

* The number set {0.1, …, 0.9} denotes the weight of DP_img (w₁), corresponding to the noise estimation of GPC as ε̂_M* = w₁·ε_{DP_img} + w₂·ε_{DP_pcd}. When w₁ = 0.0 or 1.0, GPC degenerates into DP_pcd or DP_img, respectively.

Several findings are summarized:

mag Finding 1: When both policies have moderate accuracy (e.g., >30%), GPC often achieves higher accuracy under appropriate weight configurations compared to base policies. This improvement reflects the composition of diffusion scores capturing a more generalized distribution that reduces reliance on specific conditions, consistent with the theoretical advantages of compositional models.

mag Finding 2: When one policy has significantly lower accuracy, GPC struggles to surpass the highest accuracy of the better-performing base policies. This suggests that low-accuracy scores from weaker modalities can significantly affect the joint distribution, diminishing the overall performance of the composed policy.

mag Finding 3: The improvement of GPC is always maximized when the better-performing base policy holds a larger weight in GPC. This highlights the necessity of assigning higher weights to the better-performing distribution to maximize the effectiveness of GPC, guiding the composed policy toward consensus.

These findings highlight GPC's versatility in leveraging the strengths of different conditions and the importance of appropriately tuning weights to each policy's performance.

Analysis on GPC's Superiority via Visualization

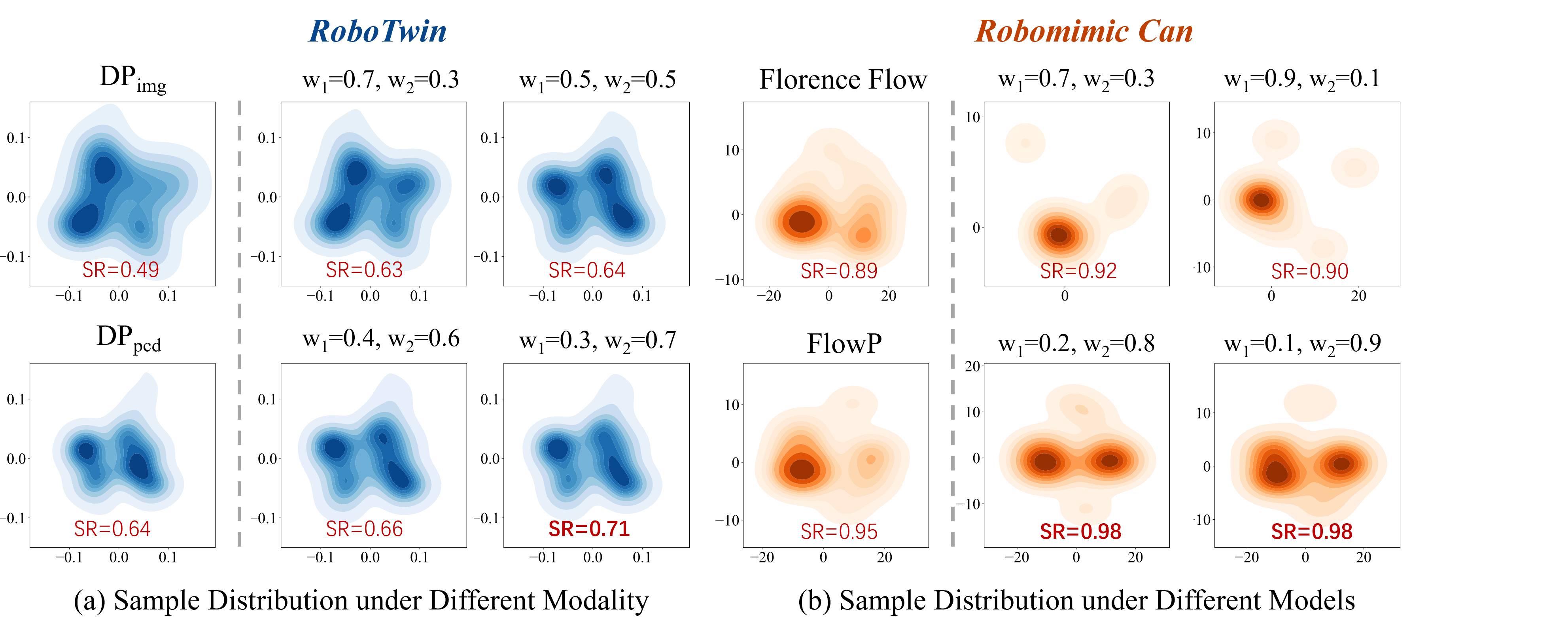
Visual Analysis of GPC under Different Compositions. GPC generalizes across (a) modalities and (b) architectures, with appropriate weighting yielding accurate distributions with better SR than individual policies.

BibTeX

@article{cao2025gpc,
      title={Compose Your Policies! Improving Diffusion-based or Flow-based Robot Policies via Test-time Distribution-level Composition}, 
      author={Jiahang Cao and Yize Huang and Hanzhong Guo and Rui Zhang and Mu Nan and Weijian Mai and Jiaxu Wang and Hao Cheng and Jingkai Sun and Gang Han and Wen Zhao and Qiang Zhang and Yijie Guo and Qihao Zheng and Chunfeng Song and Xiao Li and Ping Luo and Andrew F. Luo},
      journal={arXiv preprint arXiv:2510.01068},
      year={2025},
      url={https://arxiv.org/abs/2510.01068}, 
}